Write the Coefficient of x2 in each of the Following
A coefficient is an integer when we multiply it with the variable terms. It is usually a number that has been replaced many times by a letter in an expression. For example, ax^2 + bx + c, x is the variable, and ‘a’ and ‘b’ are the coefficients.
Table of Contents
What is a Coefficient
A coefficient refers to a quantity with a variable. The variable which does not have a number remains assumed to be having one as a Coefficient. For example, in the expression x^2 + 3, 1 is the Coefficient of x^2. In other words, a coefficient is a multiplicative factor in terms of Polynomial, and it is generally a number.
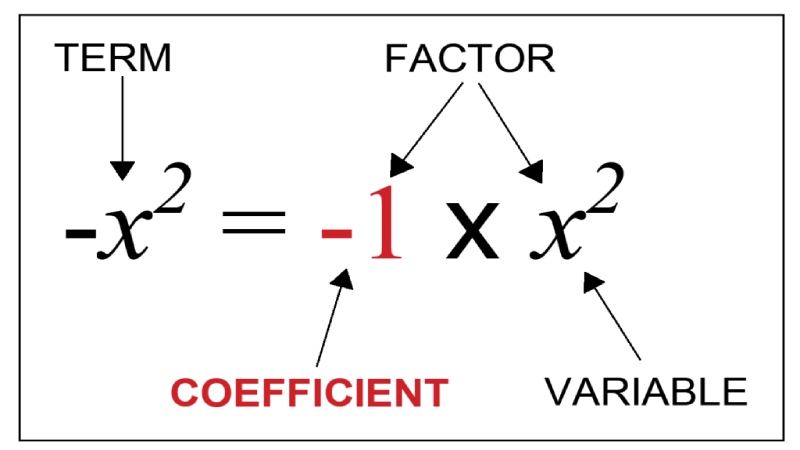
How to Find a Coefficient
The most important thing that we should remember is that it always comes with variables. For example, 5x^2 + 2y – 7. We can see that there are three terms:
Write the Coefficient if x2 in each of the Following Equation
In this question, it remains given that we have to find the coefficient x^2 among the given polynomials. So for this, we have to know that if any of the algebraic expressions remains given, like ax^3 + bx^2 + cx + d, then the Coefficient of x^2 will be numerical or constant before multiplying with x2.
- 2 + x^2 + x,
So, above equation can be written as, x^2 + x + 2 = 1 X x^2 + x + 2
When we are multiplying 1 with x2,
i.e., the Coefficient of x2 is 1.
- The given, 2 – x2 + x^3,
It can remain written off as,
X^3 – x^2 + 2
= x^3 + ( – x2 ) + 2
= x^3 + ( – 1 ) . x^2 + 2
Hence, the coefficient of x^2 is – 1.
- π/2 x^2 + x,
Here we can see π2 when it is multiplying with x^2; therefore, the Coefficient of x^2 is π2.
√2x – 1,
There is no x^2 term in this expression, so the Coefficient is 0.
To solve this question, you need o know that if the value is negative, you have to make it positive by using the minus in the brackets. Then the Coefficient becomes negative, like how we operate in problem number second.
Write the Coefficient of x2 in each of the Following Polynomials
- ( x – 1 )(3x – 4)
The given Polynomial can write like this,
(x – 1)(3x – 4) = 3x^2 – 4x – 3x + 4
= 3×2 – 7x + 4
The Coefficient of x^2 in the written Polynomial is 3.
- 12 + 3x + 5x^2
The given polynomial,
P(x) = 12 + 3x + 5^2,
The coefficient of x^2 is 5.
- X^3 – 2x^2 + 3x + 1
The coefficient of x^2 in x^3 – 2x^2 + 3x + 1 is -2.
- X^2 – x + 4
The coefficient of x^2 in x^2 – x + 4 is 1.
- 3x – 5
Given, Polynomial when we write like this, 0.x^2 + 3x – 5.
So, the Coefficient of x^2 in a given Polynomial is 0.
- The given value -3x^2
The coefficient o x^2 in the value of -3x^2 is = -3.

